VAE
Auto-Encoding Variational Bayes[1]
两位作者是来自Universiteit van Amsterdam, Machine Learning Group, Diederik P. Kingma, Max Welling.论文引用:Kingma, Diederik P. and Max Welling. “Auto-Encoding Variational Bayes.” CoRR abs/1312.6114 (2013): n. pag.
Time
- 2013.Dec
Key Words
- reparameterization of variational lower bound
- lower bound estimator
- continuous latent variable with intractable posterior
- i.i.d dataset with latent variables per datapoint
针对的问题
- how can we perform efficient approximate inference and learning with directed probabilistic models whose continuous latent variables or parameters have intractable posterior distributions?
总结
common mean-field 方法要求approximate posterior的期望的analytical solutions,通常情况下这也是intractable.
variational lower bound 的reparameterization能够产生一个简单的lower bound的可微无偏估计,SGVB(Stochastic Gradient Variational Bayes)能够用于高效的approximate posterior inference in almost any model, 能够用标准的随机梯度的方式进行优化。
通过用SGVB估计来优化识别模型,使得能够很好的执行approximate posterior inference,AEVB(auto-encoding variational bayes)算法进行推理和学习很高效。学习到的approximate posterior inference model能够用于一些任务,如recognition、denoising、representation和visualization purposes。
当这样一个神经网络用于识别模型,称之为: variational auto-encoder
在文章中,未观察到的变量\(z\)可以解释为latent representation or code, 称recognition model \(q_\phi(z|x)\) 为一个概率encoder, 称 $p_(x|z) $为一个概率decoder
Related:
- wake-sleep算法:是在线的学习算法,应用于同样的continuous latent variable models. wakel-sleep 算法用了一个recognition model来近似true posterior,缺点是要求两个目标函数同时优化,together时不能与marginal likelihood的优化一致。优点是也能应用于离散的latent variable。
- reconstruction criterion是不足以学习到有用的representation,正则化的方法能够使autoencoders学习到有用的representation,例如denoising, contractive and sparse autoencoder variants。SVGVB目标包括一个由variational bound决定的正则项。和encoder-decoder架构相关的有predictive sparse decomposition(PSD), Generative Stochastic Networks, Deep Boltzmann Machines, 这些方法是针对unnormalized models或者limited to sparse coding models,作者提出的方法是学习有向概率模型的一类通用类型。
generative model(encoder), variational approximation(decoder)
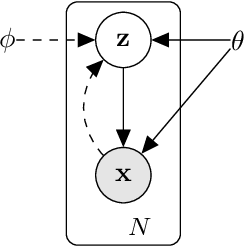
\(Fig.1^{[1]}\) Thetypeofdirected graphical model under consideration. Solid lines denote the generative model \(p_{\theta}(z) p_\theta(x|z)\), dashed lines denote the variational approximation \(q_\phi (z|x)\) to the intractable posterior $p_(z|x) $. The variational parameters \(\phi\) are learned jointly with the generative model parameters .