non-local

Non-local Neural Networks^[1]

作者是来自CMU和FAIR的Xiaolong Wang, Ross Girshick, Abhinav Gupta, Kaiming He.论文引用[1]:Wang, X. et al. “Non-local Neural Networks.” 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (2017): 7794-7803.

Time

• 2017.Nov

Key Words

• non-local 和 3D 卷积可以被视为将C2D扩展到时间维度的两种方式。
• long-range dependencies
• computes the response at a position as a weighted sum of the features at all positions
• consider all positions

动机

2. 计算长程依赖在神经网络中很重要，对于系列数据(speech, language)，循环操作是主流，对于图像数据，通过构建卷积的deep stacks，能够得到大的感受野，建模长程依赖。卷积和循环操作都处理局部相邻信息，either in space or time。因此，长程依赖只有当这些操作重复应用的时候才能捕捉到，通过数据逐步地propagating信号。重复Local operation有一些限制：首先，计算是不高效的；其次，造成了优化困难；最后，这些挑战造成了multihop dependency modeling。

总结

1. 卷积和recurrent操作都是基于处理局部相邻信息的blocks的，本文中，提出了non-local的操作，作为building blocks通用family，用于捕捉long-range dependencies。受CV中经典的non-local 方法的启发，作者的non-local的方法，计算一个位置的response as a weighted sum of the features at all positions。这个building block能够插入很多架构中，对于视频分类任务，non-local模型表现很好。

2. 在这篇文章当中，提出了non-local操作，来捕捉长程操作。提出的non-local操作是经典non-local mean操作的泛化，non-local 操作是计算一个位置的response as a weighted sum of the features at all positions。non-local操作可以插入到很多架构中，对于视频分类任务，non-local模型表现很好。set of positions可以是空间、时间或者时空；表明这个操作是可以用于图像、序列和视频的。

3. 用non-local操作有一些优点：

   • 相比于卷积和循环操作的progressive behavior，non-local操作通过计算两个任意位置的interactions，捕捉了长程依赖，不管它们之间的距离；
   • 像实验中所展示的，non-local操作是高效的，仅用少量的layers就能实现比较好的结果。
   • non-local操作保持了variable input sizes，能够很容易和其它操作结合。

4. non-local操作在视频分类、目标检测/分割/姿态估计上都有很好的结果。

5. Non-local image processing：non-local means是一个经典的滤波算法：计算图像中所有像素的weighted mean，它允许distant pixels基于patch的外观相似性来 contribute to the filtered response at a location，这个non-local滤波的想法后来发展成了BM3D：在一组相似的，non-local， patches上进行滤波操作。BM3D是一个solid image denoising baseline，block matching和神经网络用在一起，用于image enoising。non-local matching也是纹理合成、超分和impainting的精髓。

6. 图模型：长程依赖可以通过图模型进行建模，例如条件随机场(conditional random fields,CRF)，在context of DNN，一个CRF能够被利用，来后处理网络的语义分割的预测。这个iterative mean-field inference CRF可以变成一个神经网络进行训练。相比之下，作者的方法是一个简单的feedforward block for computing non-local filtering。不同于用于分割的方法，通用的component适用于分类和检测。这些方法都和一个更抽象的模型(图神经网络)相关。

7. feedforward modeling for sequences：最近出现了一个用feedforward网络来建模speech和language中序列的趋势，在这些方法中，长程依赖能够被大的感受野捕获到。这些feedforward model are amenable 来并行化执行，比广泛应用的循环网络更加高效

8. self-attention：本文的工作和最近的自注意力相关，一个自注意力模块计算the response at a position in a sequence by attending to all positions and taking their weighted average in an embedding space，自注意力可以被视为一种形式的non-local mean，在这个意义上，我们的工作**讲自注意力连接到更一般的non-local 滤波操作，这些滤波操作用于图像视频问题。

9. Interaction networks：这个工作最近提出来用于建模物理系统，它们在参与pairwise interactions的objects 图上进行操作，Hoshen提出了在多智能体预测建模环境下更高效的Vertex Attention IN，另一个变体，称为Relation Networks，在其输入的所有位置对的特征嵌入上计算一个函数。作者的方法也处理所有的pairs。当non-local 网络连接到其他方法，实验表明：模型的non-locality，和attention/interaction/relation的想法是orthogonal的，non-local 建模，一个long-time crucial element of image processing。在最近的神经网络中被忽视了。

10. 视频分类架构：一个自然的视频分类的解决方式是结合CNNs for images and RNNs for sequences。相比之下，feedforward模型通过3D卷积实现 ，3D 滤波器可以通过膨胀预训练的2D 滤波器来获得。除了原始视频进行端到端的建模之外，发现光流和轨迹也有帮助。光流和轨迹是现有的modules，能够发现长程的、non-local的依赖。

11. Non-local Neural Networks：定义深度神经网络中通用的non-local的操作: \[\mathbf{y}_i=\frac{1}{\mathcal{C}(\mathbf{x})}\sum_{\forall j}f(\mathbf{x}_i,\mathbf{x}_j)g(\mathbf{x}_j).\] 这里 \(i\)是输出位置的index，它的response被计算，\(j\)是index，来枚举所有可能的位置, \(X\)是输入信号(image,sequence,video)，\(y\)是输出信号，和\(X\)有相同的size。一个pairwise function \(f\)计算一个标量(代表relationship) between \(i\) 和 \(j\)。这个一元的function \(g\)计算输入信号在位置 \(j\)的一个representation. 这个response 通过 factor \(C(x)\)进行归一化。

    公式中的non-local是考虑了所有的位置。相比之下，一个卷积操作sums up the weighted input in a local neighborhood(卷积操作是对局部邻域的加权输入进行求和)，时间\(i\)的循环操作通常只基于当前和最新的time steps。

    这个non-local操作不同于全连接层，公式基于不同位置之间的relationships计算responses。换句话说，\(X_j\)和 \(X_i\)之间的relationship不是 \(fc\)中输入数据的function，不像non-local layers。更进一步，公式支持不同输入的size，保持了输出中的一致的size，对比之下，一个\(fc\) 层要求一个固定的size的输入/输入，丢失了位置一致性。

    一个non-local 操作是一个灵活的building block，能够很容易地和卷积/循环 layers结合，可以加入到神经网络中earlier part，不同于\(fc\)层只能用在最后。这样能够构建一个丰富的hierarchy，结合了non-local和local information。

12. Instantiations：接下来描述 \(f\)和 \(g\)的不同的版本，有趣的是，实验表明：non-local模型对这些选择不sensitive，表明这个通用的non-local behaviour是主要的理由。简单来说，考虑 \(g\)是一种线性的embedding：\(g(x_j) = W_gX_j\)，\(W_g\)是一个可学习的权重矩阵，这个通过空间上的 \(1 \times 1\)卷积或者 时空上的 \(1 \times 1 \times 1\) 卷积实现。接下来塔伦pairwiwse functin \(f\)。

    • 高斯：跟随non-local mean 和 双向的滤波器， \(f\)的一个自然的选择就是高斯函数，考虑： \[f(\mathbf{x}_i,\mathbf{x}_j)=e^{\mathbf{x}_i^T\mathbf{x}_j}.\]

    这里 \(X^T_i X_j\)是一个dot-product similarity。欧氏距离也可以用，但是dot-product执行起来更友好，归一化factor设为：\(\mathcal{C}(\mathbf{x})=\sum_{\forall j}f(\mathbf{x}_{i},\mathbf{x}_{j})\)

    • 嵌入高斯：高斯函数的一个简单的扩展是计算向量空间中的相似性： \[f(\mathbf{x}_i,\mathbf{x}_j)=e^{\theta(\mathbf{x}_i)^T\phi(\mathbf{x}_j)}.\]

    这里 \(\theta(\mathbf{x}_i) = W_\theta\mathbf{x}_i\) 和 \(\phi(\mathbf{x}_j) = W_\phi\mathbf{x}_j\) 是两个嵌入，设置 \(\mathcal{C}(\mathbf{x})=\sum_{\forall j}f(\mathbf{x}_{i},\mathbf{x}_{j}).\)

    注意到自注意力模块嵌入高斯版本的一个non-local的特例。可以从事实看出来：给定一个\(i\)，\({\frac{1}{\mathcal{C}(\mathbf{x})}}f(\mathbf{x}_{i},\mathbf{x}_{j})\) 在 dimension \(j\)上是一个 softmax 计算。因此，有 \(\mathbf{y}=softmax(\mathbf{x}^TW_\theta^TW_\phi\mathbf{x})g(\mathbf{x})\)，这个是自注意力的形式。这个工作将最近的自注意力模块和经典的non-local means联系起来，将sequential self-attention network扩展到通用的space/spacetime non-local network for image/video recognition。

    作者展示了注意力行为不是所研究的application重要。

    • Dot product：\(f\) 可以定义为： \[ f ( \mathbf{x}_{i}, \mathbf{x}_{j} )=\theta( \mathbf{x}_{i} )^{T} \phi( \mathbf{x}_{j} ). \]

    这里采用嵌入的版本，设置归一化factor \(C(x) = N\)，这里 \(N\)是 \(x\)中的位置的数量，不同于 \(f\) 的和,因为它简化了梯度计算。一个归一化是有必要的。这个 dot-product和嵌入高斯主要的不同是softmax，这个扮演了激活函数的角色。

    • Concatenation：在Relation Networks中的pairwise function用到了concatenation，评估 \(f\) 的一个 concatenation的形式：

    \[ f ( \mathbf{x}_{i}, \mathbf{x}_{j} )=\mathrm{R e L U} ( \mathbf{w}_{f}^{T} [ \theta( \mathbf{x}_{i} ), \; \phi( \mathbf{x}_{j} ) ] ). \]

    这里，[.,.]表示 concatenation，\(w_f\)是一个权重向量，将concatenated vector投射到一个标量。如上，设置 \(C(x) = N\)，这里，采用 ReLU。以上的变体展示了通用 non-local操作的灵活性。

13. Non-local Block：将non-local操作弄到一个non-local blocks，能够用于很多现有的架构，定义一个non-local block如下：

    \[ \mathbf{z}_{i}=W_{z} \mathbf{y}_{i}+\mathbf{x}_{i}, \] 这里 \("+X_i"\)表示residual connection，这个residual connection使得能够将一个新的non-local block插入到任意一个预训练的模型，不需要破坏初始的behavior(如果 \(W_z\)是初始化为0)。

    • Implementation of non-local blocks：设置 \(W_g、W_{\theta}、W_{\phi}\)的通道数为 x的一半。这个follow了bottleneck的设计，减小了block的一半的计算。这个weight matrix \(W_z\) 计算了一个position-wise embedding on \(y_i\)，匹配了\(x\)的通道。一个subsample的trick可以用于进一步减小计算。修改公式(1)为：
      \[ y_i = \frac{1} {\mathcal{C} ( \mathbf{\hat{x}} )} \sum_{\forall j} f ( \mathbf{x}_{i}, \mathbf{\hat{x}}_{j} ) g ( \mathbf{\hat{x}}_{j} ) \]

    \(\hat{x}\) 是 x的subsample。在空间域中执行这个，能够减小pairwise 大约1/4的计算。这个trick没有改变non-local的behavior。但是使得计算更稀疏。可以通过增加一个max pooling layer after \(\phi\) 和 \(g\) 来实现。

non-local

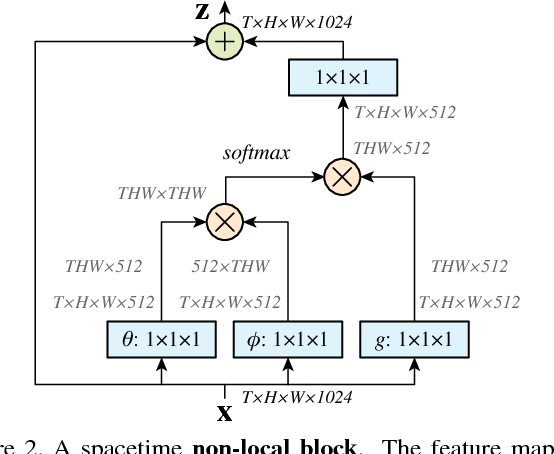
\(Fig.1^{[1]}\) A spacetime non-local block. The feature maps are shown as the shape of their tensors, e.g., \(T \times H \times W \times 1024\) for 1024 channels (proper reshaping is performed when noted). “⊗” denotes matrix multiplication, and “⊕” denotes element-wise sum. The softmax operation is performed on each row. The blue boxes denote \(1 \times 1 \times 1\) convolutions. Here we show the embedded Gaussian version, with a bottleneck of 512 channels. The vanilla Gaussian version can be done by removing \(\theta\) and \(\phi\), and the dot-product version can be done by replacing softmax with scaling by \(1/N\).